Theo định nghĩa trong toán học, hình học không gian là một nhánh của hình học nghiên cứu các đối tượng trong không gian 3 chiều Euclid. Chúng nghiên cứu các phép tính về thể tích của nhiều khối đặc khác nhau (các khối trong không gian 3 chiều) bao gồm hình chóp, hình lăng trụ và các đa diện; hình trụ tròn; hình nón; hình cụt; và khối cầu giới hạn bởi mặt cầu…
Ngày xưa chúng ta đã từng thuộc lòng những định nghĩa này… vậy mà giờ đây, đọc lại chúng thấy chẳng khác nào một người cả đời mới tụng kinh lần đầu. Câu chữ thì trúc trắc, thuật ngữ thì khó hiểu, đã vậy lại còn dài dòng rắc rối đến là đau đầu!
Tuy nhiên, ngần ấy chưa là gì so với những hình vẽ rắc rối và loạt công thức tính toán cực kỳ phức tạp dưới đây. Hẳn là nhiều bạn sinh viên sau khi xem xong những hình ảnh này sẽ thở phào nhẹ nhõm rằng: May quá, thời phải vật lộn với môn toán, từ hình học đến đại số đã qua rồi. Rất tiếc là khi nhớ lại, chúng ta đều đã “chữ thầy giả cho thầy”, chẳng còn mấy ai đọng lại trong đầu khối kiến thức mình đã từng nghiền ngẫm một thời.
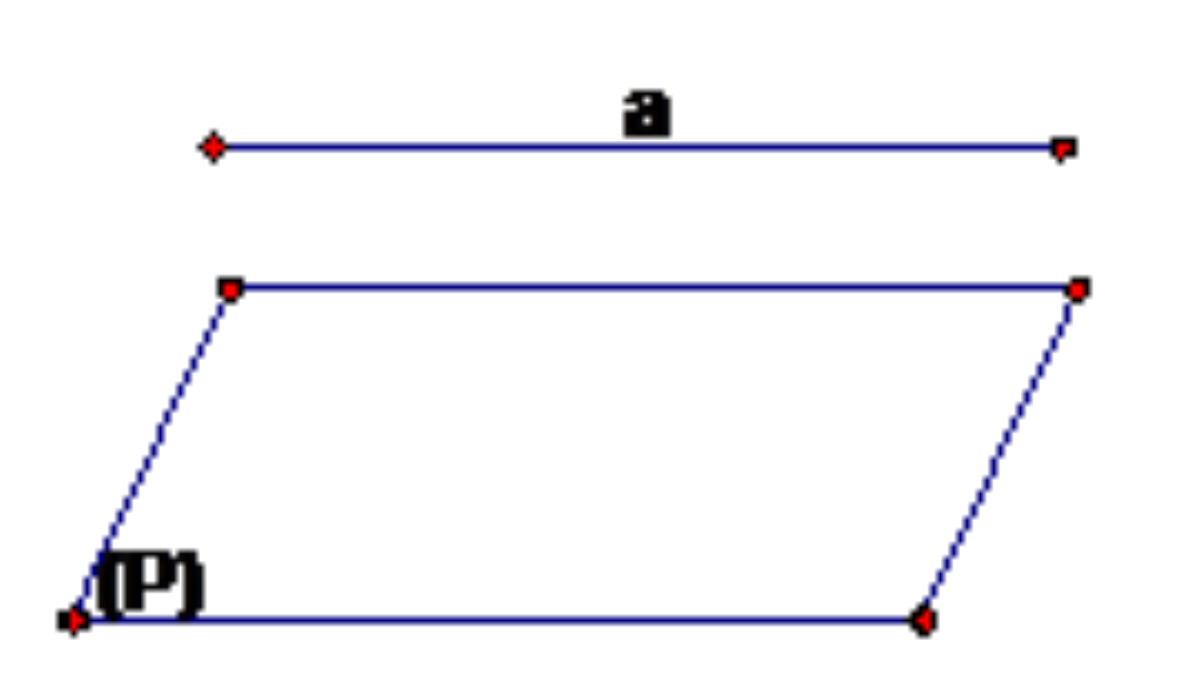
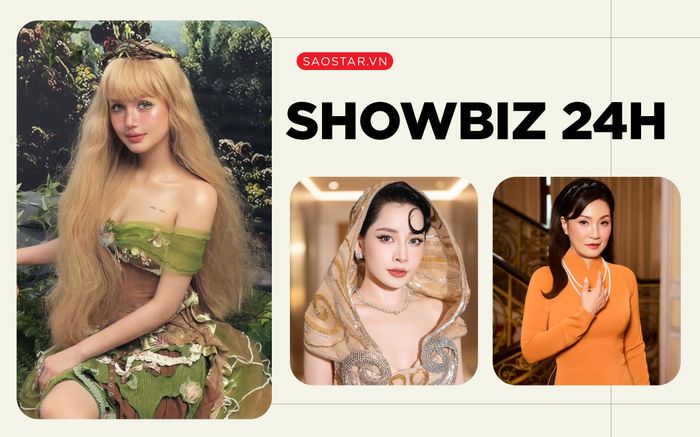
Bài học cơ bản trong hình học không gian chính là đường thẳng và mặt phẳng gọi là song song với nhau nếu chúng không có điểm nào chung.
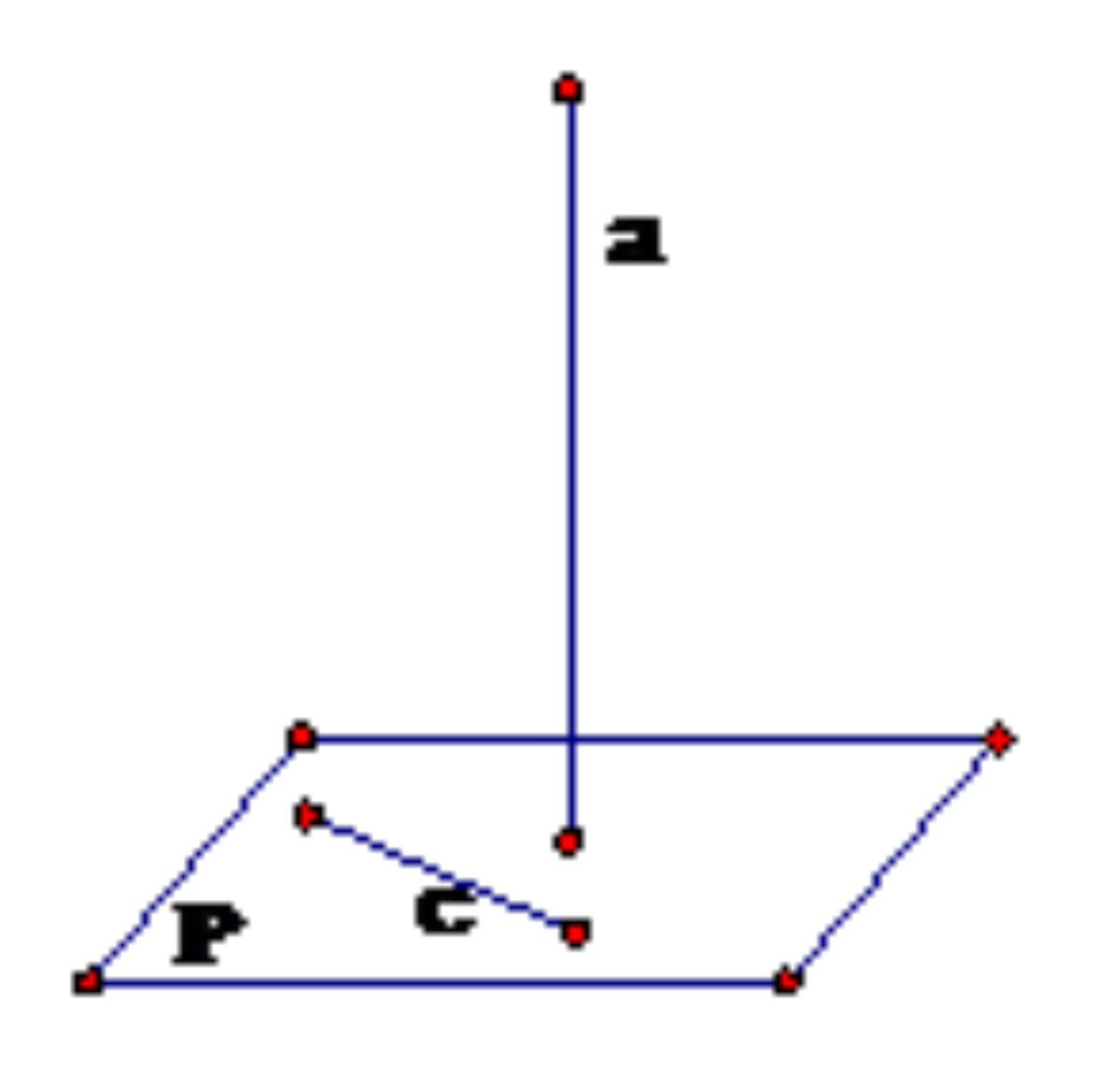
Tiếp theo, một đường thẳng được gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trên mặt phẳng đó.
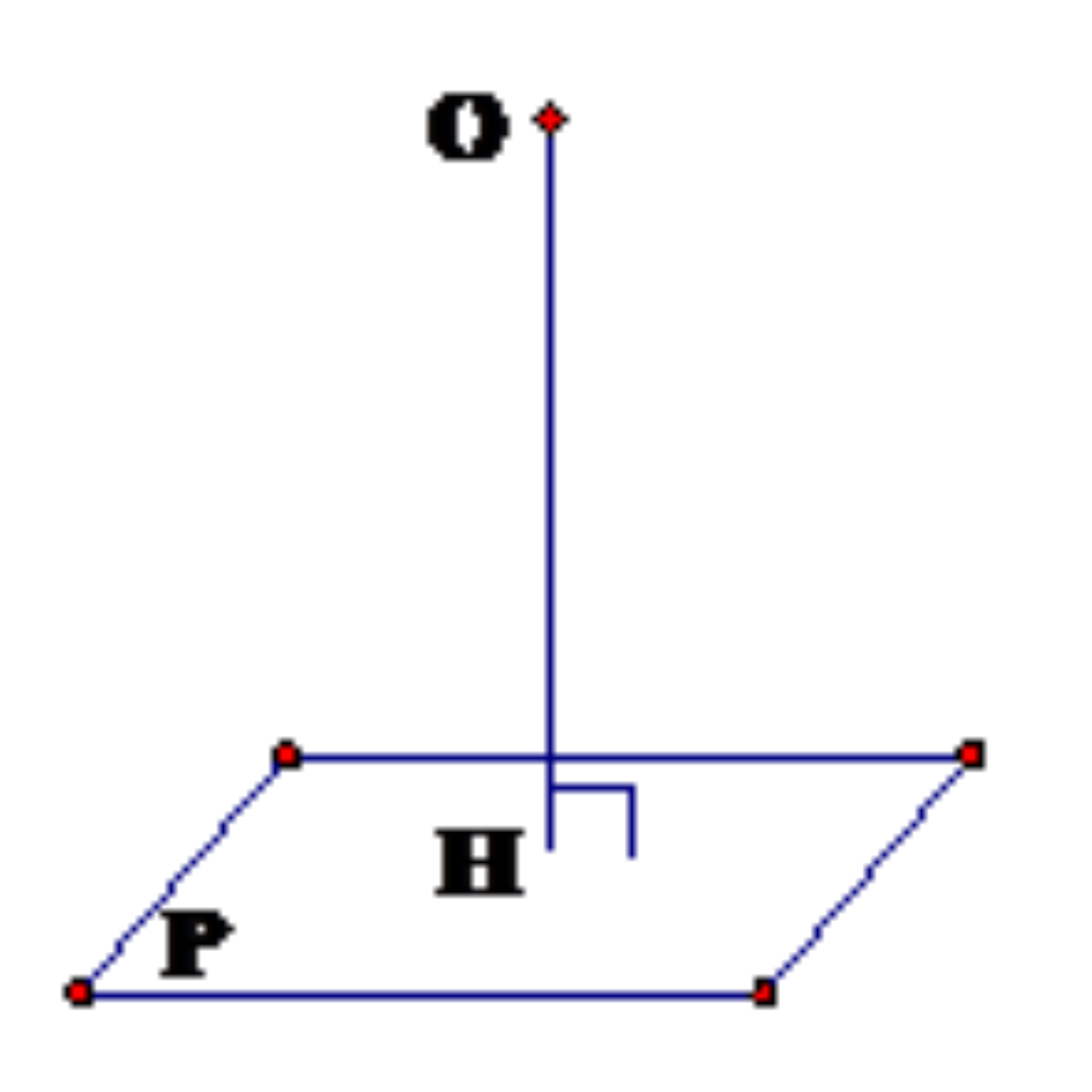
Khoảng cách từ 1 điểm tới 1 đường thẳng , đến 1 mặt phẳng: Khoảng cách từ điểm M đến đường thẳng a (hoặc đến mặt phẳng (P)) là khoảng cách giữa hai điểm M và H, trong đó H là hình chiếu của điểm M trên đường thẳng a ( hoặc trên mp(P)). Người ta thường, hình học chỉ cần có hình sẽ sáng tỏ mọi vấn đề. Có thể bạn không hiểu những con chữ kia đang truyền đạt ý nghĩa gì, đừng lo hãy nhìn hình là rõ.
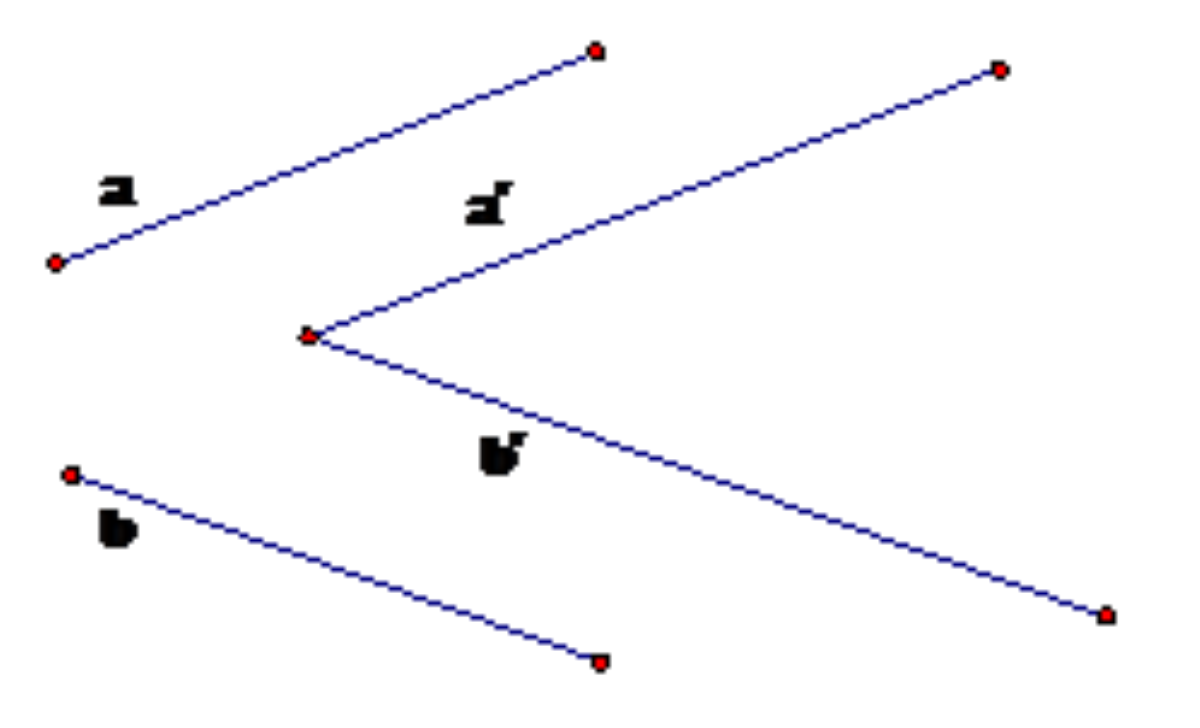
Đây là phần kiến thức sơ đẳng cuối cùng trong hình học không gian. Góc giữa hai đường thẳng a và b là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt cùng phương với a và b.
Bắt đầu là hình vẽ hoàn thiện:
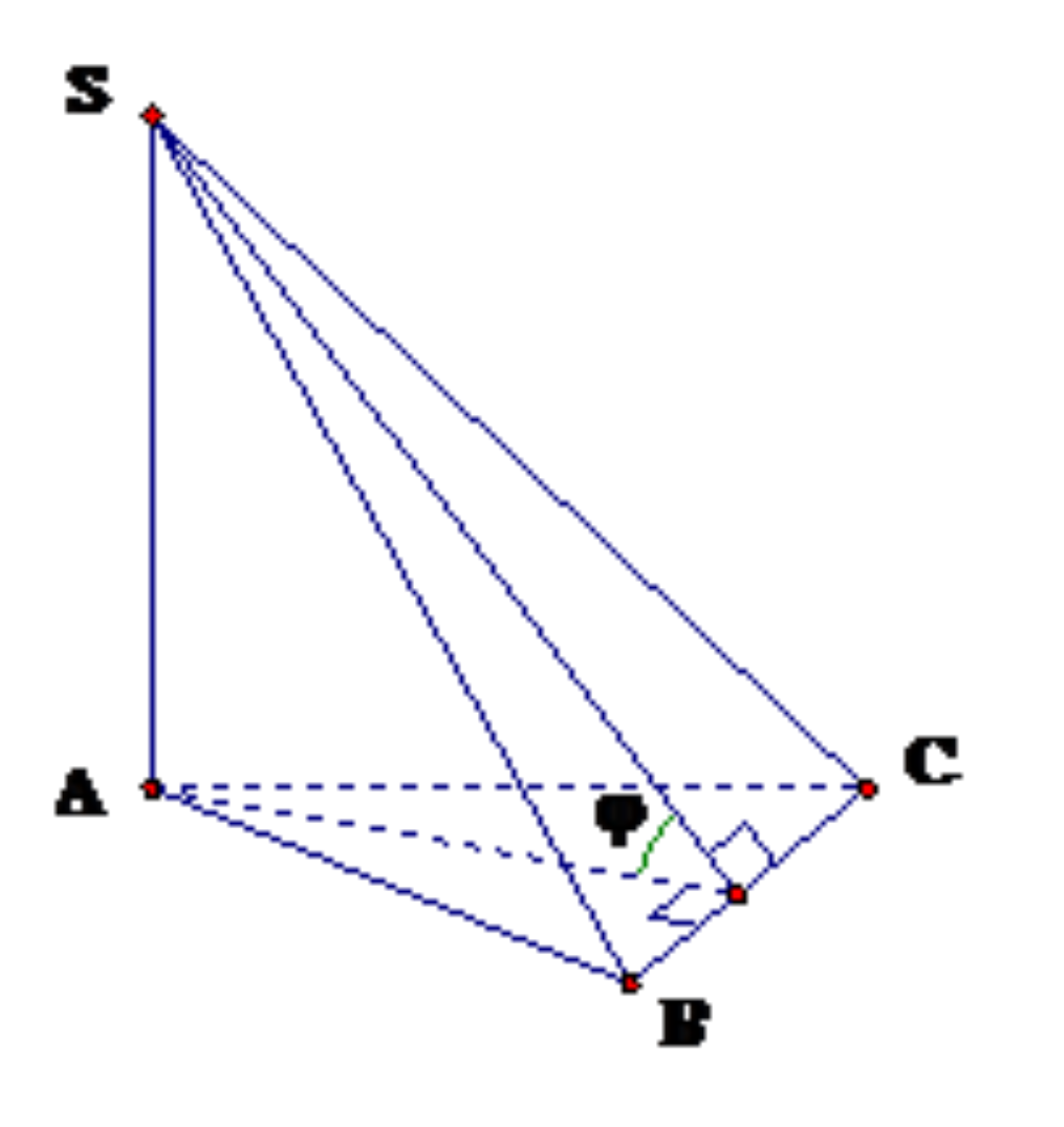

Các công thức đáng nhớ nhưng sao thấy xa lạ vậy?
Thử giải một bài toán về hình lăng trụ dưới đây: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M và N lần lượt là trung điểm của các cạnh AB và AD; H là giao điểm của CN và DM. Biết SH vuông góc với mặt phẳng (ABCD) và SH. Tính thể tích khối chóp S.CDNM và tính khoảng cách giữa hai đường thẳng DM và SC theo a.
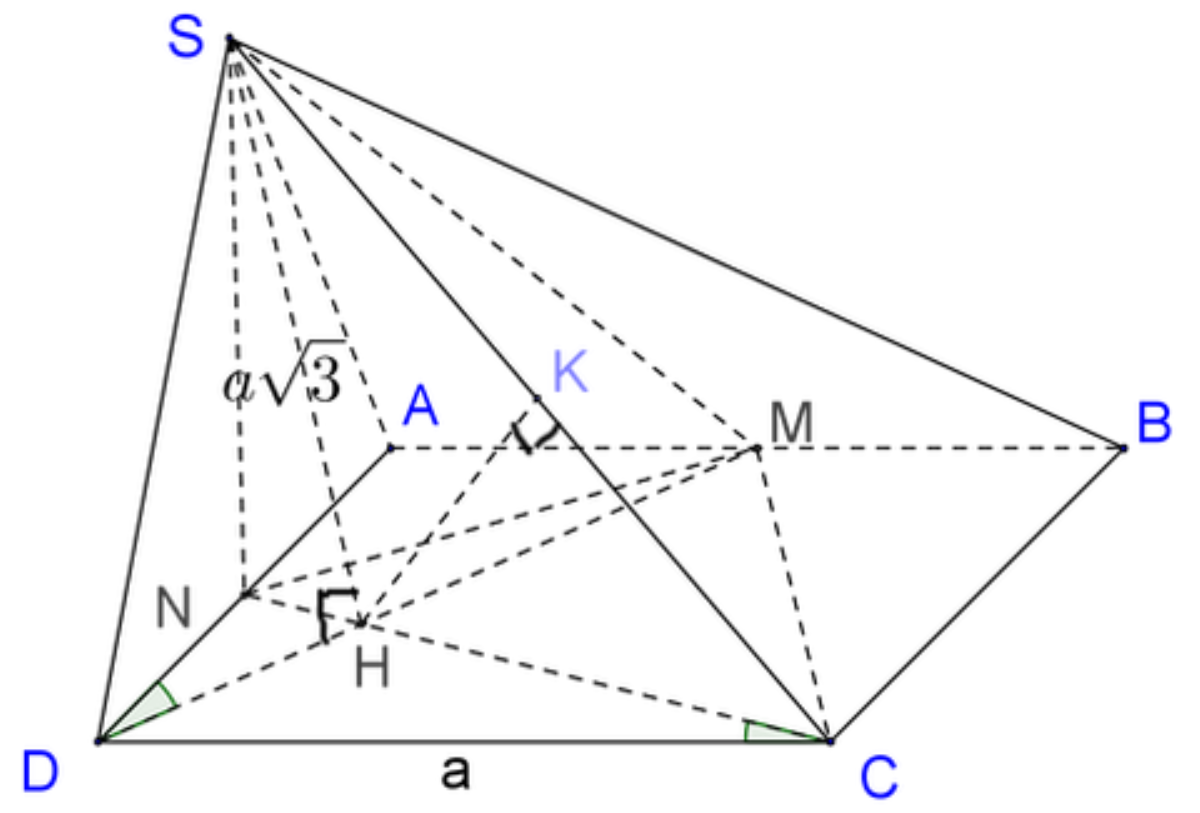
Sau khi vẽ được hình thì bắt đầu sử dụng trí tưởng tượng của mình để làm thôi!
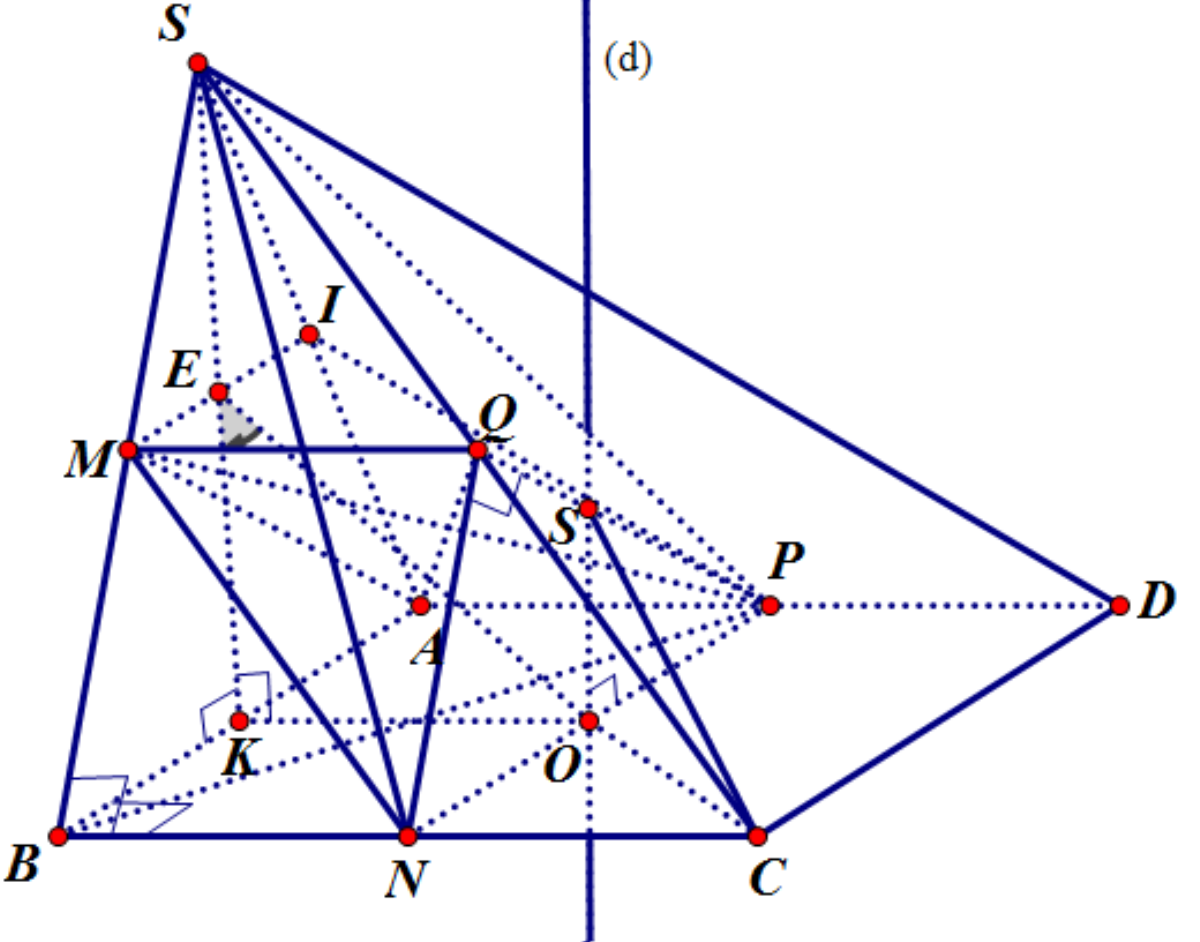
Bài này là toán cao cấp sao mà nhiều đường vậy?

Có ai nhìn thấy trang sách này quen quen không?
Công thức giải nhanh hình học không gian:
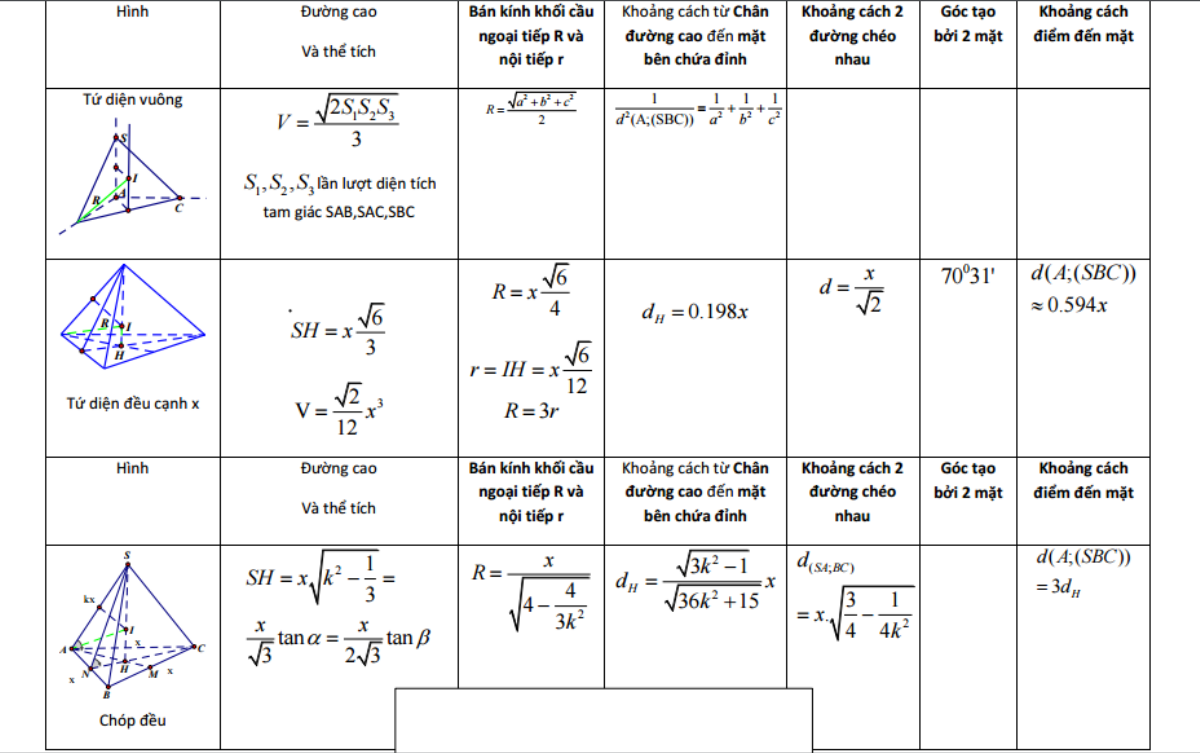
Trời ơi đúng là quên hết rồi…
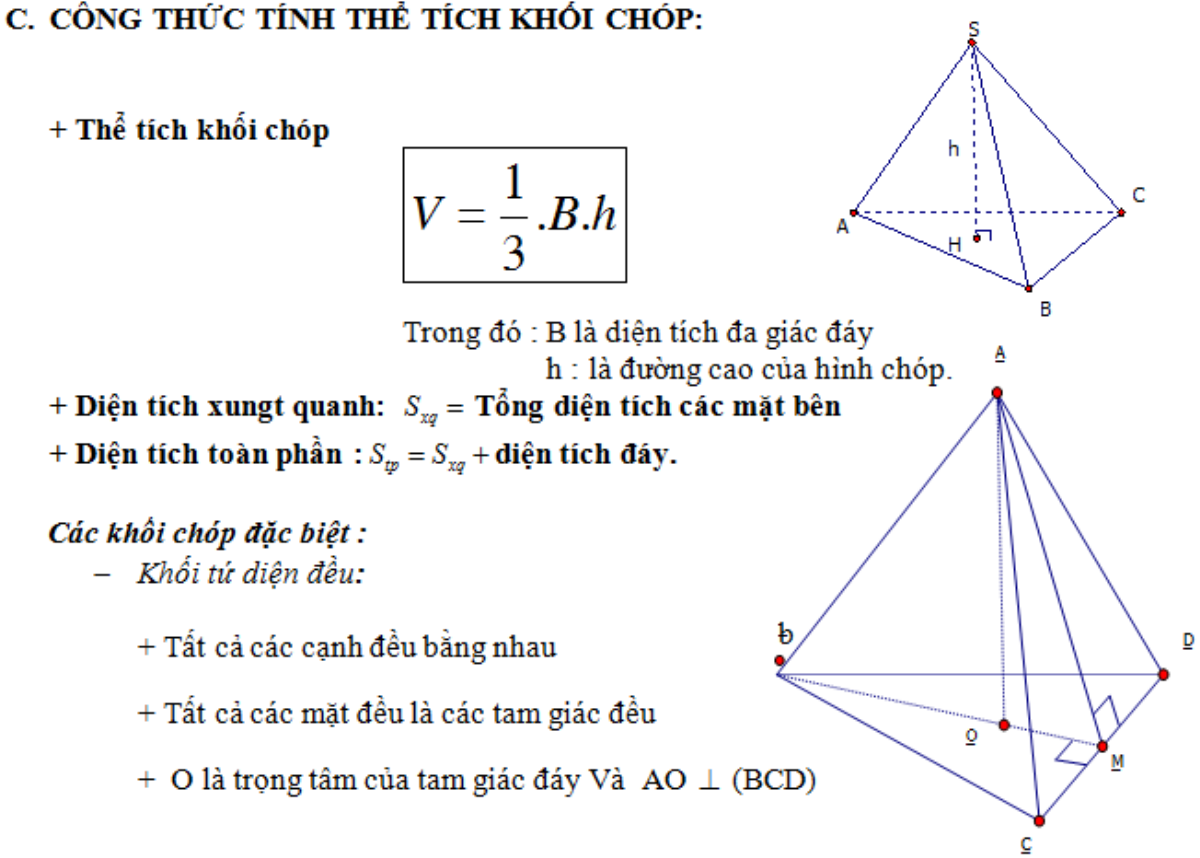
Vận dụng 100% công lực để nhớ lại công thức tính thể tích khối chóp xem nào
Cái gì mà kinh khủng thế này?
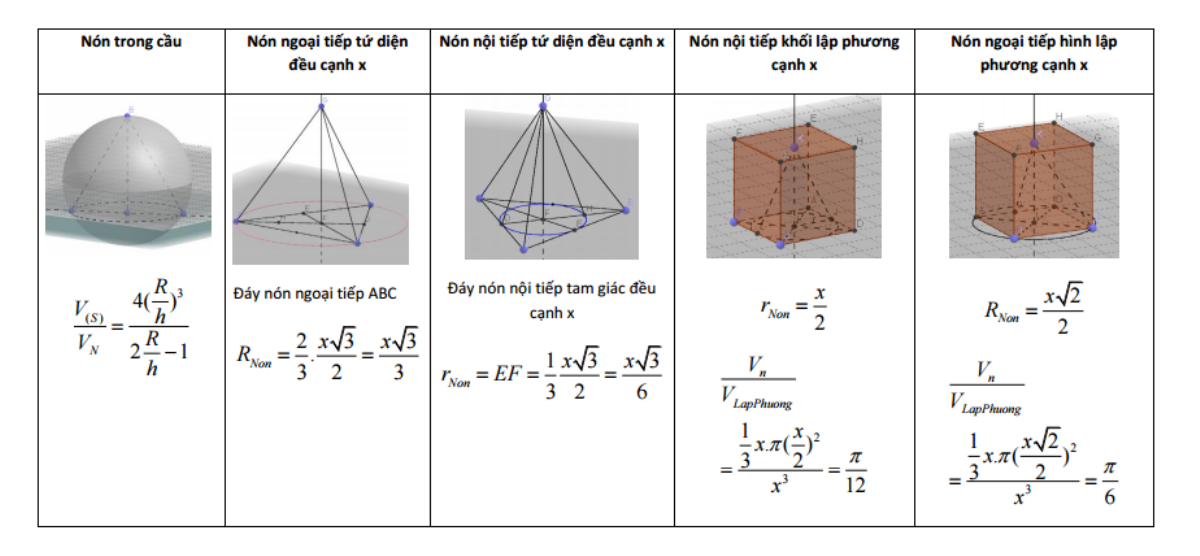
Vậy mà chúng ta đã nhớ từng ấy thứ để thi đậu ĐH cơ đấy!
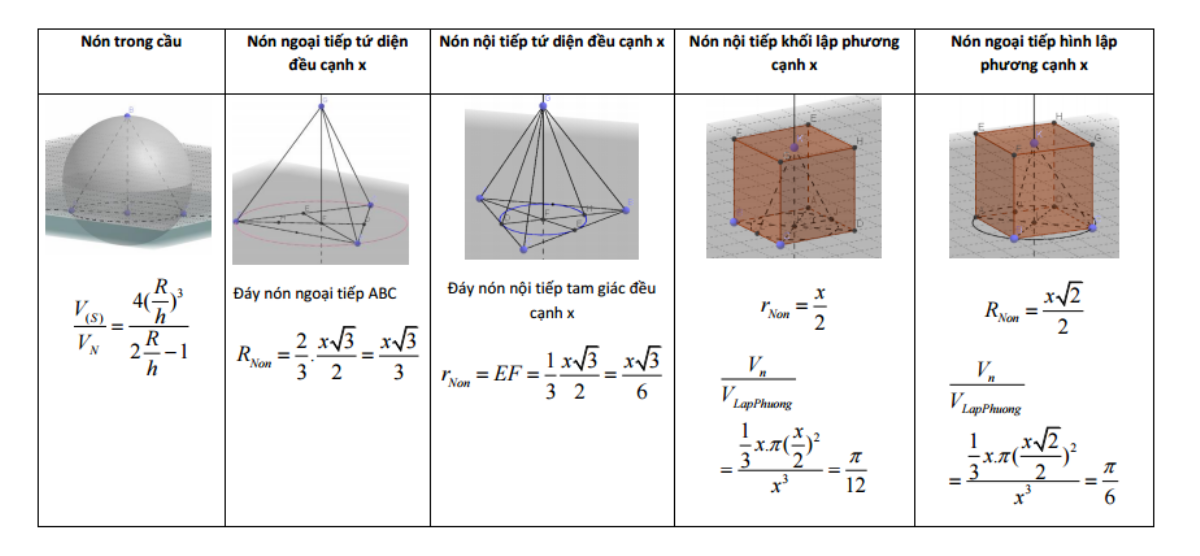
Sao lại có nhiều hình cần nhớ thế nhỉ?
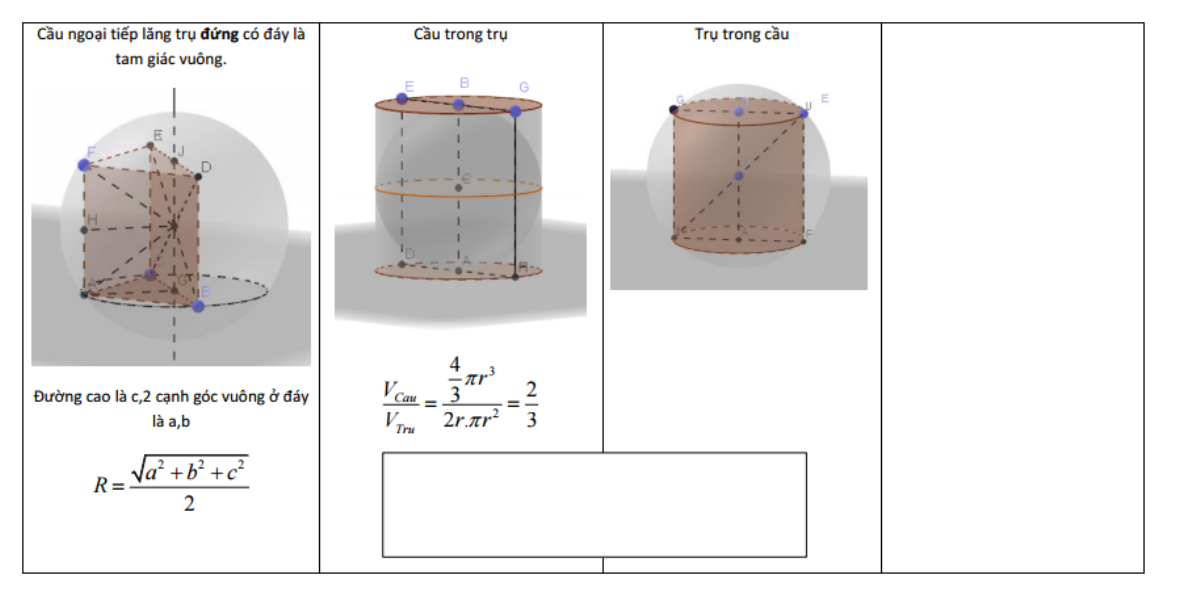
Sao ở trên mấy cái hình đơn giản thế mà cứ phải vẽ chi cho nhiều đường 3 chấm để thêm phần rối rắm?
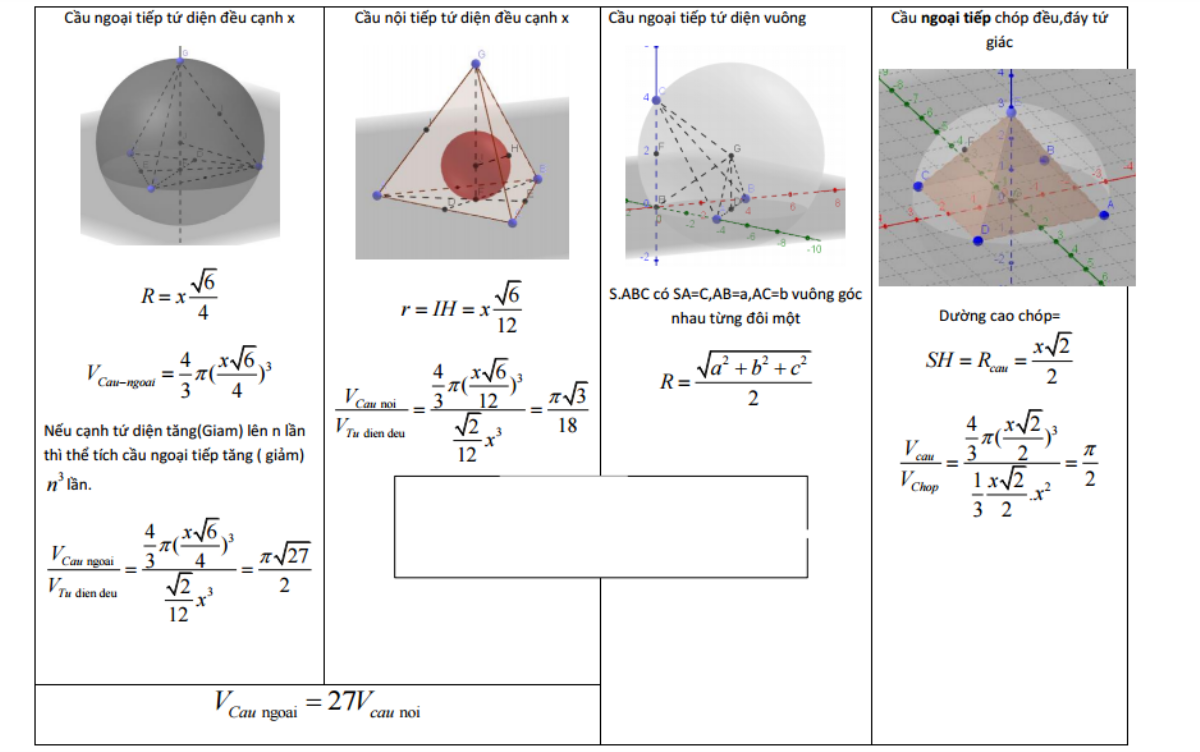
Công thức tính thể tích hình tứ diện, thể tích hình chóp nhọn sao mà khó đến thế?
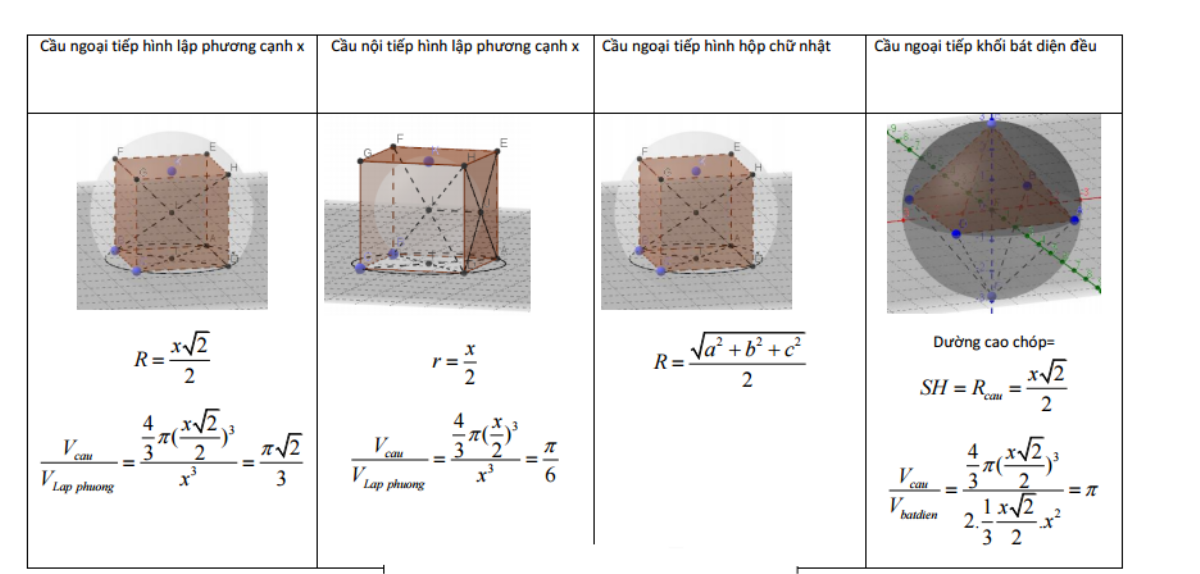
Hình cầu ngoại tiếp là gì vậy, có ai còn nhớ không?
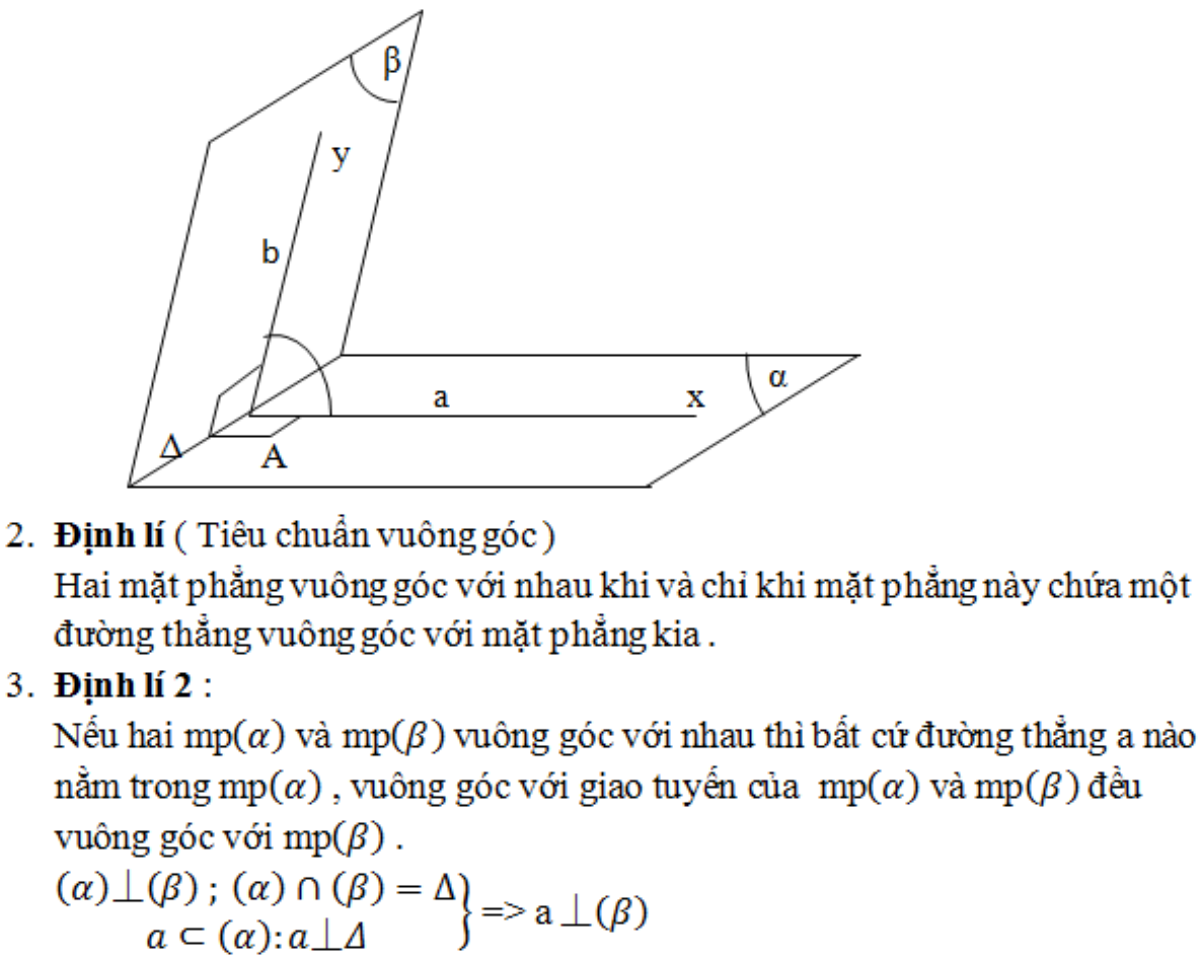
Tất cả mới chỉ là định lý trogn sách giáo khoa thôi chứ chưa phải đề thi đâu nhé!