Trao đổi với phóng viên Dân trí, GS Nguyễn Văn Tuấn Viện Garvan (Australia) cho biết, ông may mắn được cung cấp toàn bộ số liệu điểm thi của mỗi thí sinh cho mỗi môn thi trên cả nước, trong đó có tỉnh Hà Giang. Đây là dữ liệu cực kỳ quý, vì dựa vào dữ liệu này, có thể trả lời cụ thể các câu hỏi.

GS Nguyễn Văn Tuấn
Về việc dư luận, công chúng ngạc nhiên và đặt câu hỏi về kỳ thi THPT quốc gia liên quan đến điểm thi ở Hà Giang, theo ông Tuấn là hợp lý. Xét trên số liệu thực tế thì kết quả rất đáng nghi ngờ. Cho dù không thể nói có việc sửa điểm hay gì đó nhưng điểm số môn Toán của Hà Giang rất khác biệt so với quy luật chung của toàn quốc, sự khác biệt này không phải là ngẫu nhiên mà đó là sự bất thường. Rất có thể sự khác biệt này là do sự can thiệp của con người.
Theo GS Nguyễn Văn Tuấn, để xác minh điều này không khó, xác minh các thí sinh có điểm bất thường mà biểu đồ thể hiện ra một cách dễ dàng rồi xem qua lực học của các em trước đây hoặc cho các em ấy thi lại. Số lượng chỉ vài chục em, việc này hoàn toàn có thể thực hiện được.
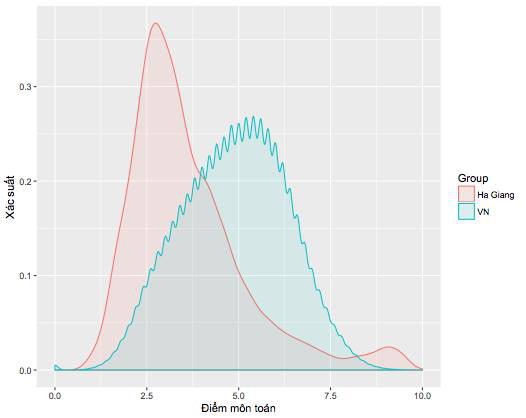
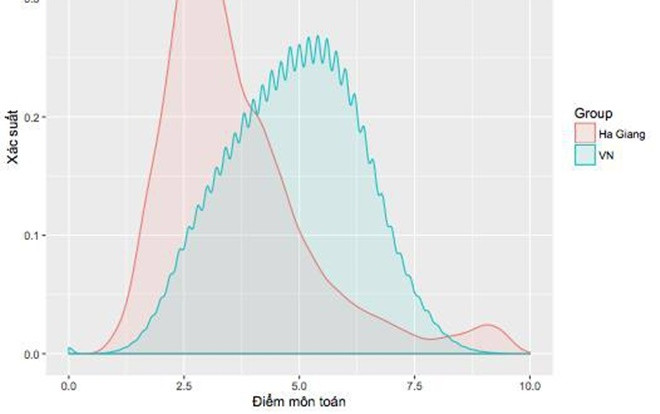
Biểu đồ này cho thấy phân bố điểm của Hà Giang (màu hồng) và của cả nước (màu xanh). Có hai điểm chính có thể rút ra từ hình này: (a) Điểm trung vị của Hà Giang là khoảng 3.2, thấp hơn điểm của toàn quốc (trung vị khoảng 5.0); (b) Phân bố điểm của Hà Giang có vẻ bất thường ở điểm từ 8 đến 10. Chú ý đường biểu diễn của Hà Giang “nhô lên” trong khi đáng lí ra phải smooth như cả nước.
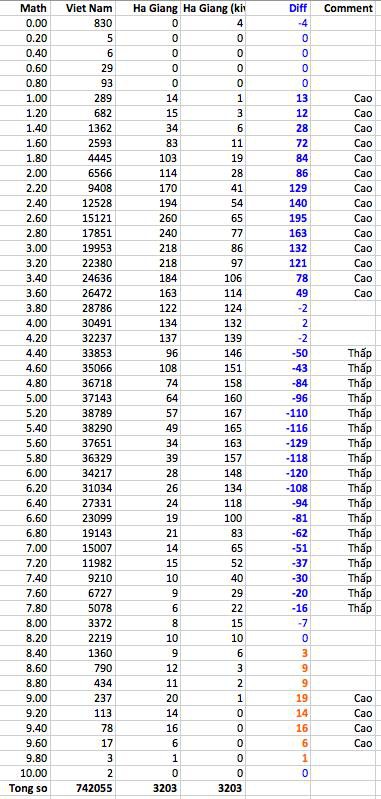
Để kiểm tra kĩ hơn chỗ “nhô lên” đó, cần phải phân tích so sánh giữa phân bố điểm thực tế của Hà Giang và điểm của cả nước.. Ví dụ, chú ý cột số 4 (Ha Giang), ở điểm 9, nếu theo phân bố quốc gia thì chúng ta kì vọng Hà Giang có 1 em đạt điểm này. Thế nhưng trong thực tế, Hà Giang có đến 20 em đạt điểm 9 (cột 3).
Nếu phân bố điểm thi của Hà Giang tương đương với phân bố của cả nước, thì cột thứ 5 sẽ gần bằng 0. Nhưng chúng ta thấy trong thực tế thì không phải vậy, và vài chỗ lệch thể hiện rất rõ sau đây:
- Ở điểm thấp (từ 1 đến 3.6), số thí sinh Hà Giang cao hơn so với giá trị kì vọng
- Nhưng ở điểm cao hơn (từ 4.0 đến 7.8) thì số thí sinh Hà Giang thấp hơn giá trị kì vọng của cả nước
- Nhưng điều thú vị nhất là ở điểm cao 'top' (từ 8.6 đến 9.6) số thí sinh Hà Giang cao hơn so với phân bố cả nước. Nếu theo xu hướng của cả nước, Hà Giang chỉ có 7 thí sinh ở ngưỡng điểm 8.6 đến 9.6, nhưng trong thực tế con số thí sinh đạt điểm này là 72, tức cao gấp ~10 lần so với cả nước.
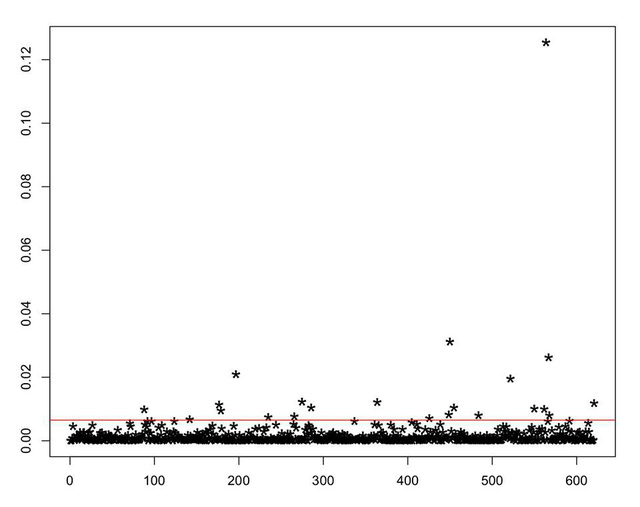 Biểu đồ này có mục đích nhận dạng cụ thể thí sinh nào có điểm cao bất thường. GS Tuấn tìm mối liên hệ giữa môn Toán và các môn khác; sau đó dựa vào điểm của các môn khác tính giá trị kì vọng điểm môn toán cho mỗi em sau đó mình so sánh điểm kì vọng và điểm thực tế. Nếu điểm thực tế cao gấp 4 độ lệch chuẩn kì vọng là bất thường. Tại sao 4? Vì 4 độ lệch chuẩn là 99.99%, nên nếu cao hơn con số này thì xem như là “quá cỡ” (khó tin).
Biểu đồ này có mục đích nhận dạng cụ thể thí sinh nào có điểm cao bất thường. GS Tuấn tìm mối liên hệ giữa môn Toán và các môn khác; sau đó dựa vào điểm của các môn khác tính giá trị kì vọng điểm môn toán cho mỗi em sau đó mình so sánh điểm kì vọng và điểm thực tế. Nếu điểm thực tế cao gấp 4 độ lệch chuẩn kì vọng là bất thường. Tại sao 4? Vì 4 độ lệch chuẩn là 99.99%, nên nếu cao hơn con số này thì xem như là “quá cỡ” (khó tin).
Đường màu đỏ là giá trị kỳ vọng (đáng lý là phải vậy). Chỉ cần 1 cá nhân là đã phải nghi ngờ, và ở đây là khoảng 20 em trên đường màu đỏ, vượt xa kỳ vọng có thể xem là bất bình thường, đặc biệt có một thí sinh “ngồi” riêng ở vị trí rất xa các bạn khác. Đây là những con số phải nghi ngờ ngay.
Có trên 950 thí sinh điểm 0 môn Toán là bất thường
GS Nguyễn Văn Tuấn phân tích, môn Toán có 50 câu, mỗi câu có 4 lựa chọn. Do đó, xác suất sai cho mỗi câu hỏi là 3/4. Xác suất một thí sinh sai tất cả 50 câu phải là p = (3/4)^50 = 0.0000005663 (giả định độc lập). Nhưng ở đây, chúng ta có n=917484 thí sinh. Gọi x là số thí sinh có điểm 0, lí thuyết phân bố nhị phân cho biết giá trị trung bình của x là mean(x) = np = 0.51 và độ lệch chuẩn sd = sqrt(n*p*(1-p)) = 0.72.
Dùng hai tham số này để mô phỏng thì chúng ta có thể tính xác suất có 951 thí sinh có điểm 0: 1-pnorm(951, mean=0.51, sd=0.72) kết quả là 0. Một cách khác là giá trị kì vọng trong số 1 triệu thí sinh thi, thì tối đa chỉ có 3 thí sinh với điểm 0 môn toán. Nhưng trong thực tế, kì thi này ghi nhận có đến 951 thí sinh có điểm 0. Và, đó là điều bất thường.